Jeep problem

Short description: Mathematics and car problem

Plot of amount of fuel f vs distance from origin d for exploring (1–3) and crossing (I–III) versions of the jeep problem for three units of fuel – coloured arrows denote depots, diagonal segments denote travel and vertical segments denote fuel transfer

The jeep problem, desert crossing problem or exploration problem is a mathematics problem in which a jeep must maximize the distance it can travel into a desert with a given quantity of fuel. The jeep can only carry a fixed and limited amount of fuel, but it can leave fuel and collect fuel at fuel dumps anywhere in the desert.

The problem first appeared in the 9th-century collection Propositiones ad Acuendos Juvenes (Problems to Sharpen the Young), attributed to Alcuin, with the puzzle being about a travelling camel eating grain. The De viribus quantitatis (c. 1500) of Luca Pacioli also discusses the problem. A modern treatment was given by N. J. Fine in 1947.

Variations of the problem are the camel and bananas problem where a merchant must maximize the number of bananas transported to a market using a camel that feeds on the bananas, the travelers across the desert problem where a number of travellers must all reach a destination and can only exchange supplies rather than leaving them, and the cars across the desert problem which again can only exchange their fuel, but where empty cars can be abandoned. This final problem has similarities to the operation of a multistage rocket.

Problem

Plot to scale of the Exploring (top) and Crossing (bottom) versions of the jeep problem for three units of fuel. The horizontal axis denotes distance and vertical axis denotes time. Vertical coloured line segments denote stashing fuel and horizontal ones denote travel using withdrawn fuel. Coloured numbers denote units of fuel stashed at that moment.

There are n units of fuel stored at a fixed base. The jeep can carry at most 1 unit of fuel at any time, and can travel 1 unit of distance on 1 unit of fuel (the jeep's fuel consumption is assumed to be constant). At any point in a trip the jeep may leave any amount of fuel that it is carrying at a fuel dump, or may collect any amount of fuel that was left at a fuel dump on a previous trip, as long as its fuel load never exceeds 1 unit. There are two variants of the problem:

• Exploring the desert – the jeep must return to the base at the end of every trip.
• Crossing the desert – the jeep must return to the base at the end of every trip except for the final trip, when the jeep travels as far as it can before running out of fuel.

In either case the objective is to maximize the distance traveled by the jeep on its final trip. Alternatively, the objective may be to find the least amount of fuel required to produce a final trip of a given distance.

Variations

In the classic problem the fuel in the jeep and at fuel dumps is treated as a continuous quantity. More complex variations on the problem have been proposed in which the fuel can only be left or collected in discrete amounts.

In the camel and bananas problem, the merchant has n units of bananas. The camel can carry at most 1 unit of bananas at any time, and can travel 1 unit of distance on 1 unit of bananas. The market is at m units of distance away. At any point in a trip the camel may leave any amount of bananas that it is carrying at a camp post, or may collect any amount of bananas that was left at a camp post on a previous trip, as long as its banana load never exceeds 1 unit. The problem asks for the maximum units of bananas that can be transported to the market.

In the travelers across the desert problem, the starting base has unlimited units of supplies. Each traveler can carry at most 1 unit of supplies at any time, and can travel 1 unit of distance on 1 unit of supplies. The other base is at m units of distance away. Contrary to the previous two problems, the travelers can't leave supplies in the desert; However, at any point in a trip, accompanying travelers can transfer supplies among themselves, as long as each traveler never carries more than 1 unit of supplies. Each returning traveler must have enough supplies on the way back. The problem asks for the minimum number of accompanying travelers needed to reach the other base. A variant of this problem gives the total number of travelers available, and asks for the maximum distance that can be reached.

In the cars across the desert problem, the starting base has unlimited units of fuel. Each car can carry at most 1 unit of supplies at any time, and can travel 1 unit of distance on 1 unit of fuel. The other base is at m units of distance away. The cars can't leave fuel in the desert; However, at any point in a trip, accompanying cars can transfer fuel among themselves, as long as each car never carries more than 1 unit of fuel. Empty cars with no fuel are abandoned in the desert. The problem asks for the minimum number of accompanying cars needed to reach the other base. A variant of this problem gives the total number of cars available, and asks for the maximum distance that can be reached.

Solution

Solution to "exploring the desert" variant for n = 3, showing fuel contents of jeep and fuel dumps at start of each trip and at turnround point on each trip.

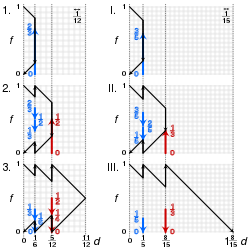
A strategy that maximizes the distance traveled on the final trip for the "exploring the desert" variant is as follows:

• The jeep makes n trips. On each trip it starts from base with 1 unit of fuel.
• On the first trip the jeep travels a distance of 1/(2n) units and leaves (n − 1)/n units of fuel at a fuel dump. The jeep still has 1/(2n) units of fuel – just enough to return to base.
• On each of the subsequent n − 1 trips the jeep collects 1/(2n) units of fuel from this first fuel dump on the way out, so that it leaves the fuel dump carrying 1 unit of fuel. It also collects 1/(2n) units of fuel from this first fuel dump on the way back, which is just enough fuel to return to base.
• On the second trip the jeep travels to the first fuel dump and refuels. It then travels a distance of 1/(2n − 2) units and leaves (n − 2)/(n − 1) units of fuel at a second fuel dump. The jeep still has 1/(2n − 2) units of fuel, which is just enough to return to the first fuel dump. Here it collects 1/(2n) units of fuel, which is just enough fuel to return to base.
• On each of the subsequent n − 2 trips the jeep collects 1/(2n − 2) units of fuel from this second fuel dump on the way out, so that it leaves the fuel dump carrying 1 unit of fuel. It also collects 1/(2n − 2) units of fuel from the second fuel dump on the way back, which is just enough fuel to return to the first fuel dump.
• The jeep continues in this way, so that on trip k it establishes a new kth fuel dump at a distance of 1/(2n − 2k + 2) units from the previous fuel dump and leaves (n − k)/(n − k + 1) units of fuel there. On each of the subsequent n − k trips it collects 1/(2n − 2k + 2) units of fuel from the kth dump on its way out and another 1/(2n − 2k + 2) units of fuel on its way back.

When the jeep starts its final trip, there are n − 1 fuel dumps. The farthest contains 1/2 of a unit of fuel, the next farthest contain 1/3 of a unit of fuel, and so on, and the nearest fuel dump has just 1/n units of fuel left. Together with 1 unit of fuel with which it starts from base, this means that the jeep can travel a total round trip distance of

[math]\displaystyle{ 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} = \sum_{k=1}^n \frac{1}{k} \equiv 2\times\mathrm{explore}(n) }[/math]

units on its final trip (the maximum distance traveled into the desert is half of this). It collects half of the remaining fuel at each dump on the way out, which fills its tank. After leaving the farthest fuel dump it travels 1/2 a unit further into the desert and then returns to the farthest fuel dump. It collects the remaining fuel from each fuel dump on the way back, which is just enough to reach the next fuel dump or, in the final step, to return to base.

Solution to "crossing the desert" variant for n = 3, showing fuel contents of jeep and fuel dumps at start of each trip, at turnaround point on first two trips, and at end of final trip.

The distance travelled on the last trip is the nth harmonic number, H_n. As the harmonic numbers are unbounded, it is possible to exceed any given distance on the final trip, as along as sufficient fuel is available at the base. However, the amount of fuel required and the number of fuel dumps both increase exponentially with the distance to be traveled.

The "crossing the desert" variant can be solved with a similar strategy, except that there is now no requirement to collect fuel on the way back on the final trip. So on trip k the jeep establishes a new kth fuel dump at a distance of 1/(2n − 2k + 1) units from the previous fuel dump and leaves (2n − 2k − 1)/(2n − 2k + 1) units of fuel there. On each of the next n − k − 1 trips it collects 1/(2n − 2k + 1) units of fuel from the kth dump on its way out and another 1/(2n − 2k + 1) units of fuel on its way back.

Now when the jeep starts its final trip, there are n − 1 fuel dumps. The farthest contains 1/3 of a unit of fuel, the next farthest contain 1/5 of a unit of fuel, and so on, and the nearest fuel dump has just 1/(2n − 1) units of fuel left. Together with 1 unit of fuel with which it starts from base, this means that the jeep can travel a total distance of

[math]\displaystyle{ 1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{2n-1} = \sum_{k=1}^n \frac{1}{2k-1}=H_{2n-1}-\frac{1}{2}H_{n-1} \equiv \mathrm{cross}(n) }[/math]

units on its final trip. It collects all of the remaining fuel at each dump on the way out, which fills its tank. After leaving the farthest fuel dump it travels a further distance of 1 unit.

Note that

[math]\displaystyle{ \mathrm{cross}(n)=\sum_{k=1}^n \frac{1}{2k-1} \gt \sum_{k=1}^n \frac{1}{2k} = \frac{1}{2}H_{n}=\mathrm{explore}(n) }[/math]

so it is possible in theory to cross a desert of any size given enough fuel at the base. As before, the amount of fuel required and the number of fuel dumps both increase exponentially with the distance to be traveled.

In summary, the maximum distance reachable by the jeep (with a fuel capacity for 1 unit of distance at any time) in n trips (with n-1 midway fuel dumps and consuming a total of n units of fuel) is

• [math]\displaystyle{ \mathrm{explore}(n)= \frac{1}{2}H_{n}=\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \cdots + \frac{1}{2n} }[/math], for exploring the desert where the jeep must return to the base at the end of every trip;
• [math]\displaystyle{ \mathrm{cross}(n)=H_{2n-1}-\frac{1}{2}H_{n-1}=1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{2n-1} }[/math], for crossing the desert where the jeep must return to the base at the end of every trip except for the final trip, when the jeep travels as far as it can before running out of fuel.

Here [math]\displaystyle{ H_n=1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} }[/math] is the nth harmonic number.

Continuous amount of fuel

The number of fuel units available at the base need not be an integer. In the general case, the maximum distance achievable for the "explore the desert" problem with n units of fuel is

[math]\displaystyle{ \mathrm{explore}(n) = \int_0^n \frac{\mathrm{d}f}{2 \lceil n-f \rceil} }[/math]

with the first fuel dump located at [math]\displaystyle{ \{n\}/(2 \lceil n \rceil) }[/math] units of distance away from the starting base, the second one at [math]\displaystyle{ 1/(2 \lceil n \rceil-2) }[/math] units of distance away from the first fuel dump, the third one at [math]\displaystyle{ 1/(2 \lceil n \rceil-4) }[/math] units of distance away from the second fuel dump, and so on. Here [math]\displaystyle{ \{n\}=n-\lfloor n \rfloor }[/math] is the fractional part of n.

The maximum distance achievable for the "cross the desert" problem with n units of fuel is

[math]\displaystyle{ \mathrm{cross}(n) = \int_0^n \frac{\mathrm{d}f}{2 \lceil n-f \rceil - 1} }[/math]

with the first fuel dump located at [math]\displaystyle{ \{n\}/(2 \lceil n \rceil-1) }[/math] units of distance away from the starting base, the second one at [math]\displaystyle{ 1/(2 \lceil n \rceil-3) }[/math] units of distance away from the first fuel dump, the third one at [math]\displaystyle{ 1/(2 \lceil n \rceil-5) }[/math] units of distance away from the second fuel dump, and so on. Here [math]\displaystyle{ \{n\}=n-\lfloor n \rfloor }[/math] is the fractional part of n.

Other variants of the problem

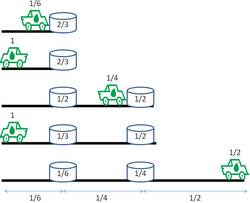
In the camel and bananas problem, assuming the merchant has a total of n=7/3 units of bananas at the starting base and the market is at m units of distance away:

• If [math]\displaystyle{ m\gt \mathrm{cross}(n)=1/15+1/3+1 }[/math], no solution exists for this problem;
• If [math]\displaystyle{ m\leq \mathrm{cross}(n)-\mathrm{cross}(\lfloor n\rfloor)=1/15 }[/math], no midway camp post is necessary for the transport, and the distance m will be repeated for [math]\displaystyle{ 2 \lceil n \rceil-1=5 }[/math] times by the camel, so the maximum amount of bananas tranported to the market is [math]\displaystyle{ n-m\times (2 \lceil n \rceil-1)=7/3-5m }[/math];
• If [math]\displaystyle{ \mathrm{cross}(n)-\mathrm{cross}(\lfloor n\rfloor)\lt m\leq \mathrm{cross}(n) }[/math], the optimal solution to transport that maximum amount of bananas requires some midway camp posts:
  1. For m=1/4<(1/3+1/15), only one midway camp post is necessary at a distance of 1/15 units away from the starting base, where a total of 2 units of bananas will accrue. The distance from the camp post to the market is (1/4-1/15), which will be repeated 3 times by the camel, and the maximum amount of bananas tranported to the market is 2-(1/4-1/15)*3=1.45 units;
  2. For m=1/2>(1/3+1/15), another midway camp post is necessary at a distance of 1/3 units from the first camp post, where a total of 1 unit of bananas will accrue. The distance from the second camp post to the market is [1/2-(1/3+1/15)], which will be traveled only once by the camel, and the maximum amount of bananas tranported to the market is 1-[1/2-(1/3+1/15)]*1=0.9 units.

If the camel is required to eventually return to the starting base, then the [math]\displaystyle{ \mathrm{explore}(n) }[/math] function applies (still assuming n=7/3):

• If [math]\displaystyle{ m\gt \mathrm{explore}(n)=1/18+1/4+1/2 }[/math], no solution exists for this problem;
• If [math]\displaystyle{ m\leq \mathrm{explore}(n)-\mathrm{explore}(\lfloor n\rfloor)=1/18 }[/math], no midway camp post is necessary for the transport, and the distance m will be repeated for [math]\displaystyle{ 2 \lceil n \rceil=6 }[/math] times by the camel, so the maximum amount of bananas tranported to the market is [math]\displaystyle{ n-m\times (2 \lceil n \rceil)=7/3-6m }[/math];
• If [math]\displaystyle{ \mathrm{explore}(n)-\mathrm{explore}(\lfloor n\rfloor)\lt m\leq \mathrm{explore}(n) }[/math], the optimal solution to transport that maximum amount of bananas requires some midway camp posts:
  1. For m=1/4<(1/4+1/18), only one midway camp post is necessary at a distance of 1/18 units away from the starting base, where a total of 2 units of bananas (plus 1/18 units for the camel's final return) will accrue. The distance from the camp post to the market is (1/4-1/18), which will be repeated 4 times by the camel, and the maximum amount of bananas tranported to the market is 2-(1/4-1/18)*4=1.22 units;
  2. For m=1/2>(1/4+1/18), another midway camp post is necessary at a distance of 1/4 units from the first camp post, where a total of 1 unit of bananas (plus 1/4 units for the camel's final return) will accrue. The distance from the second camp post to the market is [1/2-(1/4+1/18)], which will be repeated twice by the camel, and the maximum amount of bananas tranported to the market is 1-[1/2-(1/4+1/18)]*2=0.61 units.

In the travelers across the desert problem, assume that n travelers set out from the starting base with n units of supplies. After 1/(n+1) units of distance, they would have already consumed n/(n+1) units of supplies; At this point, one of the travelers should return with 1/(n+1) units of supplies, leaving the group exactly (n-1) units of supplies so that each remaining traveler carries exactly one unit of supplies. The group then travels another 1/(n+1) units of distance, consuming (n-1)/(n+1) units of supplies; At this point, one of the remaining travelers should return with 2/(n+1) units of supplies to safely get back to the starting base, leaving the group exactly (n-2) units of supplies. The group keeps moving 1/(n+1) units of distance and reducing one traveler, until there is only one traveler left carrying exactly one unit of supplies. Finally, this traveler can travel one unit of distance to reach the farthest point. In total, the longest distance n travelers can reach is

[math]\displaystyle{ \mathrm{travel}(n)=\frac{n-1}{n+1}+1=2-\frac{2}{n+1} }[/math]

Equating this to m, one may solve for the minimum number of travelers needed to travel m units of distance. Note that solutions only exist for m<2.

If the last and final traveler also needs to return to the starting base, then he would only travel 1/(n+1) unit alone so that he has n/(n+1) units of supply to return, so the longest distance n travelers can reach is

[math]\displaystyle{ \mathrm{travel_{return}}(n)=\frac{n}{n+1}=1-\frac{1}{n+1} }[/math]

Equating this to m, one may solve for the minimum number of travelers needed to travel m units of distance. Note that solutions only exist for m<1.

In the cars across the desert problem, assume that n cars set out from the starting base with n units of fuel. After 1/n units of distance, the group would have already consumed exactly one unit of fuel; At this point, they should transfer fuel between them, leave an empty car behind, and carry (n-1) units of fuel among (n-1) cars. After another 1/(n-1) units of distance, the group would have consumed another one unit of fuel; Again, they should transfer fuel, leave an empty car behind, and carry (n-2) units of fuel among (n-2) cars. The group keeps moving and reducing one car, until there is only one car left carrying exactly one unit of fuel. Finally, this car can travel one unit of distance to reach the farthest point. In total, the longest distance n cars can reach is the nth harmonic number:

[math]\displaystyle{ H_n=1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} }[/math]

Equating this to m, one may solve for the minimum number of cars needed to travel m units of distance.

Order independence

Note that the order of the jeep trips is not fixed. For example in the "exploring the desert" version of the problem, the jeep could make n − 1 round-trips between the base and the first fuel dump, leaving (n − 1) / n units of fuel at the fuel dump each time and then make an n-th trip one-way to the first fuel dump, thus arriving there with a total of (n − 1) + 1/(2n) units of fuel available. The 1/(2n) units are saved for the return trip to base at the very end and the other n − 1 units of fuel are used to move fuel between the first and second fuel dump, using n − 2 round-trips and then an (n−1)-th trip one-way to the second fuel dump. And so on.

Practical applications

In Operation Black Buck One, the attacking Vulcan was refuelled seven times on the outward journey and once on the return journey. Grey lines indicate reserve aircraft to replace casualties.

The problem can have a practical application in wartime situations, especially with respect to fuel efficiency. In the context of the bombing of Japan in World War II by B-29s, Robert McNamara says in the film The Fog of War that understanding the fuel efficiency issue caused by having to transport the fuel to forward bases was the main reason why the strategy of launching bombing raids from mainland China was abandoned in favor of the island hopping strategy:

"We had to fly those planes from the bases in Kansas to India. Then we had to fly fuel over the hump into China. [...] We were supposed to take these B-29s—there were no tanker aircraft there. We were to fill them with fuel, fly from India to Chengtu; offload the fuel; fly back to India; make enough missions to build up fuel in Chengtu; fly to Yawata, Japan ; bomb the steel mills; and go back to India. We had so little training on this problem of maximizing [fuel] efficiency, we actually found to get some of the B-29s back instead of offloading fuel, they had to take it on. To make a long story short, it wasn't worth a damn. And it was LeMay who really came to that conclusion, and led the Chiefs to move the whole thing to the Marianas, which devastated Japan."

(The atomic bombing missions at the end of World War II were flown using B-29 Superfortresses from the Pacific island of Tinian in the Northern Marianas Islands.)

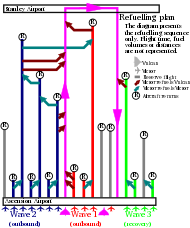
See also Operation Black Buck for an application of these ideas. In these missions, conducted during the Falklands War, the Royal Air Force used air to air refueling by staging tankers to enable the Vulcan bombers based on Ascension Island to bomb targets in the Falkland Islands.

See also

• Harmonic series (mathematics)
• Optimization (mathematics)